고유값과 고유벡터

nxn 크기의 정사각 행렬 A

n×1 크기의 열 벡터 $\vec{x}$

ex) A가 3x3 행렬이라면 x는 3x1

 

A $\vec{x}$ 와 $\vec{x}$ 가 아래의 식을 만족할 때,

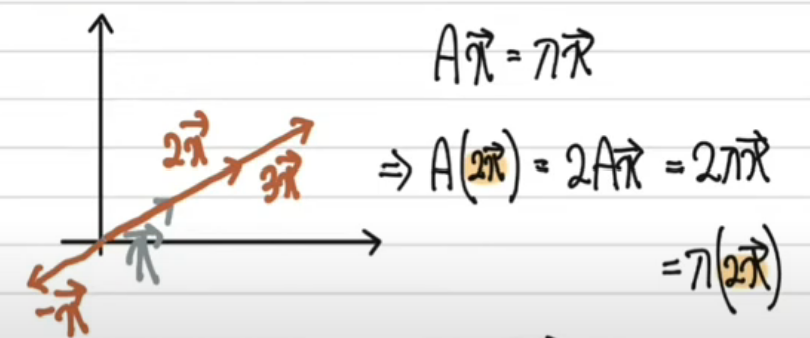
즉 A $\vec{x}$ 와 $\vec{x}$ 가 평행하고, $\vec{x}$ 를 실수 배만큼 늘리거나 줄여서 A $\vec{x}$ 와 같게 만들 수 상황이 발생할 때,

\(A \vec{x} = λ\vec{x}\)

위의 식에서

λ는 A의 고유값

$\vec{x}$ 를 A의 λ에 대한 고유벡터라고 한다.

 

 

주의사항

• 영벡터는 고유벡터로 볼 수 없다. (무조건 식이 성립하여, 모든 실수가 고유값이 되어버림)
• 고유벡터는 무수히 많다.( $\vec{x}$ 가 λ에 대한 고유벡터라면, k $\vec{x}$ 또한 λ에 대한 고유벡터)

 

 

고유값 λ구하기

\(A \vec{x} = λ\vec{x}\)

위 식을 변형하면

\(A - λI)\vec{x} = 0 \)라는 식이 된다.

즉,  \(A - λI)\vec{x} = 0 \)라는 식을 만족하는 영벡터가 아닌 $\vec{x}$가 존재하는 실수 λ를 고유값이라고 한다.

 

또한, A - λI는 역행렬을 갖지 않는다.

양쪽에 (A - λI)의 역행렬을 곱할 시, $\vec{x}$=0이라는 식이 성립되어 모순이 발생한다.

역행렬을 갖지 않는다는 말은 즉 행렬식이 0임을 뜻하므로

| A - λI | = 0 이라는 결론이 나온다.

 

따라서, | A - λI | = 0를 만족하는 λ를 고유값이라고 한다.

 

 

 

예를 들어

A = $ \begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix} $의 고유값을 구할 때,

A - λI = $ \begin{pmatrix} -λ & 1 \\ 1 & -λ \end{pmatrix} $

| A - λI | = λ제곱 - 1

λ제곱 = 플러스마이너스1

 

 

예시

1. 2x2 행렬의 경우:
   • AAA가 2x2 행렬이면, xxx는 2x1 벡터가 됩니다.
   • 예: A=(1234)A = \begin{pmatrix} 1 & 2 \\ 3 & 4 \end{pmatrix}A=(13​24​), x=(x1x2)x = \begin{pmatrix} x_1 \\ x_2 \end{pmatrix}x=(x1​x2​​)
2. 3x3 행렬의 경우:
   • AAA가 3x3 행렬이면, xxx는 3x1 벡터가 됩니다.
   • 예: A=(100020003)A = \begin{pmatrix} 1 & 0 & 0 \\ 0 & 2 & 0 \\ 0 & 0 & 3 \end{pmatrix}A=​100​020​003​​, x=(x1x2x3)x = \begin{pmatrix} x_1 \\ x_2 \\ x_3 \end{pmatrix}x=​x1​x2​x3​​​

결론

행렬 AAA와 벡터 xxx의 크기는 문제에 따라 달라질 수 있으며, 반드시 2x2 또는 2x1일 필요는 없습니다. 중요한 점은 AAA가 정사각 행렬이어야 하고, xxx는 이에 대응하는 열 벡터여야 한다는 것입니다.

λ